




















Eu criei este site com a intenção de compartilhar o meu vasto conhecimento de algoritmos do cubo 3x3 de forma organizada, visto a grande variedade dos mesmos. As dicas mostradas daqui em diante fazem parte do Método CFOP de SpeedCubing.

CFOP é um dos, se não o método mais famoso utilizado para resolver o Cubo Mágico, principalmente pela sua simplicidade e a diversidade de algoritmos.
"C" significa Cross (Cruz), e é o primeiro passo do método CFOP, onde você escolhe uma peça central para formar uma cruz que consiste nesse centro junto a quatro peças de borda da mesma cor. As peças da cruz são inseridas no slot de forma que a segunda cor da peça esteja conectada a sua respectiva peça central. Por ser o primeiro passo para resolver o cubo, e que ele está todo embaralhado com diversas combinações, não há necessidade de listar algoritmos específicos que resolvem a Cruz, tornando a ser uma etapa mais intuitiva.
"F" equivale a F2L, ou First 2 Layers (Primeiras 2 Camadas), é a próxima etapa depois de fazer a Cruz. Nesta parte do método você deve encontrar e juntar as peças de canto e de borda que se complementam formando pares, para assim inserí-los nos respectivos slots. Diante das inúmeras possibilidades de onde as peças podem se situar, esta etapa é majoritariamente intuitiva. Porém, os resolvedores de cubo criaram algoritmos para cada caso de F2L, mas já que são muito específicos e variados, não serão mostrados aqui.
"O" significa OLL, ou Orientation of the Last Layer (Orientação da Última Camada), e acontece depois de resolver as Primeiras 2 Camadas. Utilizando um dos 57 algoritmos de OLL, você deve resolver o lado oposto a Cruz que você fez no início. Não há segredo, pois agora você deve observar, reconhecer o padrão e executar o movimento o mais rápido possível utilizando-se da sua memória muscular. Existe um método utilizado para formar casos considerados bons (peças de borda orientadas), para depois resolvê-los com as bordas já orientadas.
A seguir, dois algoritmos básicos que orientarão todas as quatro peças de borda do topo:
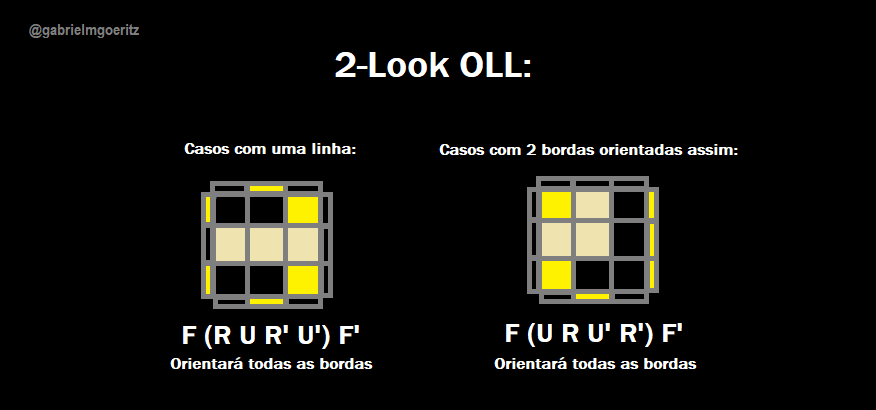
"P" equivale a PLL, ou Permutation of the Last Layer (Permutação da Última Camada), e é a última etapa do CFOP. Depois de OLL, você utilizará um dos 21 algoritmos que permutará a última camada. E assim, você resolve o Cubo. Assim como OLL, existem dois algoritmos que resolvem os cantos da última camada, para depois você finalizar com um algoritmo mais fácil, resolvendo o Cubo.
A seguir, dois algoritmos básicos que resolverão todas as quatro peças de canto do topo:
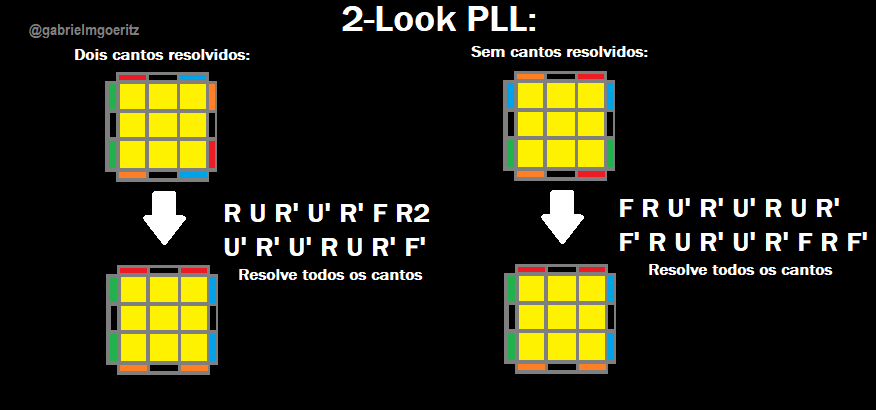
A comunidade utiliza-se de nomenclaturas para cada movimento realizável em um cubo mágico, partindo dos nomes de direções em inglês, e no sentido horário (Right, Left, Front, Up...). Um movimento sozinho representa uma giro de 90° daquela face do cubo.
A imagem a seguir demonstra 7 nomenclaturas que ajudarão a entender os algoritmos do Cubo Mágico 3x3 mostrados daqui pra frente:
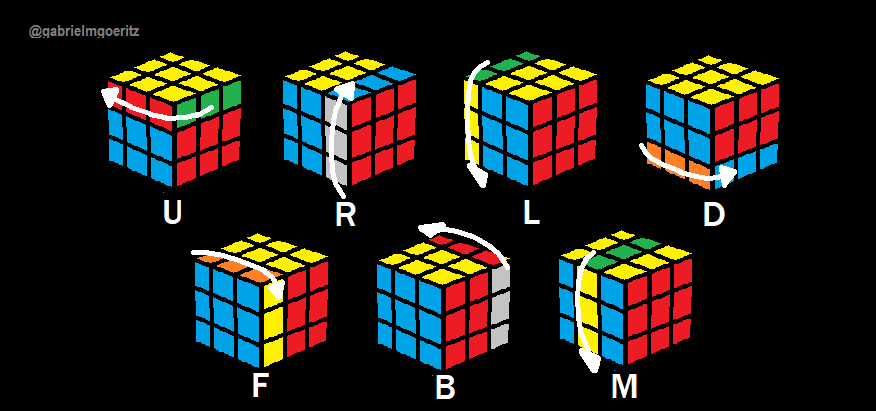
O apóstrofo (') ao lado das letras representa um movimento de 90° daquela face porém em sentido anti-horário:
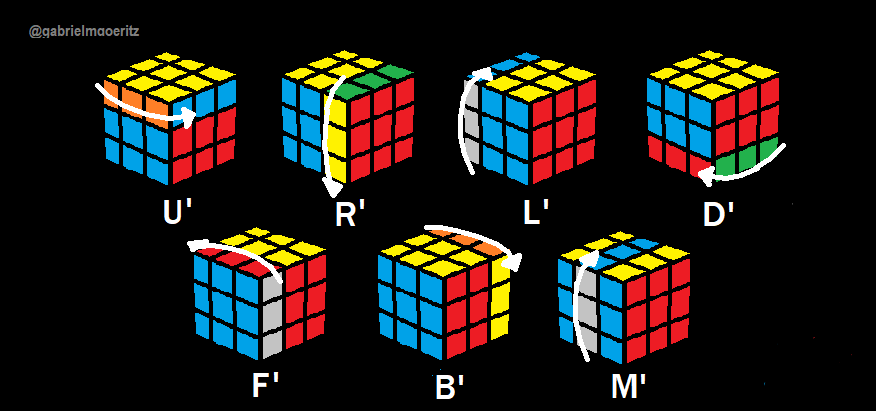
Letras seguidas de um "2 (dois)" representam um movimento duplo, ou seja, um giro de 180° para qualquer sentido, horário ou anti-horário.
Orientação da Última Camada
| OLL | Algoritmo |
|---|---|
 |
F (U R U' R') F' |
 |
F (R U R U')2 F' |
 |
R U R' U R U' R' U' (R' F R F') |
 |
f' (L' U' L U) f |

| r U R' U' M U R U' R' |

| r U2 R' U' R U' r' |
 |
l' U2 L U L' U l |
 |
(F R' F' R) (U R U' R') |
 |
L' U' L U' L' U L U L F' L' F |
 |
F' (L' U' L U)2 F |
 |
F (R U R' U') F' |
 |
(R U R' U') (R' F R F') |
 |
(R U R' U') M' (U R U' R') |
 |
F (U R U' R')2 F' |

| F (R U R' U')3 F' |
 |
R U2 R2 U' R2 U' R2 U2 R |
 |
R U R' U R U2 R' |
 |
R U2 R' U' R U' R' |
 |
F R' x U' L U R U' r' |
 |
L F R' F' L' F R F' |
 |
R2 D R' U2 R D' R' U2 R' |
Permutação da Última Camada
| PLL | Algoritmo |
|---|---|
 |
x R2 F R F' R U2 r' U r U2 |
 |
R U R' F' R U R' U' R' F R2 U' R' |
 |
x L2 D2 L' U' L D2 L' U L' |
 |
x L U' L D2 L' U L D2 L2 |
 |
R U R' U' R' F R2 U' R' U' R U R' F' |
 |
F R U' R' U' R U R' F' R U R' U' R' F R F' |
 |
M2 U M2 U2 M2 U M2 |
 |
R U' R U R U R U' R' U' R2 |
 |
M2 U' M U2 M' U' M2 |
 |
M2 U M2 U M' U2 M2 U2 M' |
 |
R U' R U R' D R D' R U' D R2 U R2 D' R2 |
 |
r' D' F r U' r' F' D r2 U r' U' r' F r F' |